---

Introduction

NumPy (Numerical Python) is an open-source Python library that’s used in almost every field of science and engineering.

It's a Python toolbox filled with handy tools for handling numbers and data. With NumPy, you get a super versatile array that can do all sorts of math, help you rearrange data, sort things neatly, pick out what you need, read and write stuff, and even perform cool tasks like Fourier transforms, basic math, stats, and random simulations.

In simple terms, NumPy is your go-to kit for doing smart math and data stuff in Python.

Prerequisites

You’ll need to know the basics of Python.

Installing and Importing NumPy

Before we dive into the exciting world of NumPy, we need to ensure it's properly installed and ready to use in your Python environment. Follow these steps to install and import NumPy:

Installing NumPy

Using pip (Python Package Installer)

Open your terminal or command prompt and enter the following command:

pip install numpy

Using conda (Anaconda)

If you are using Anaconda Python package management, you can install NumPy with conda:

conda install numpy

Importing NumPy

Once NumPy is installed, Import NumPy at the beginning of your code like this:

import numpy as np

The import statement allows you to access NumPy's functions and features using the shorthand np.

Numpy array:

What's an Array in NumPy?

An array is a central data structure of the NumPy library.

An array in NumPy is like a special grid that holds data. It's organized, and all the stuff inside it is of the same type, referred to as the array dtype.

One way we can initialize NumPy arrays is from Python lists and using nested lists for two- or higher-dimensional data.

The rank of the array is the number of dimensions(basically a number of nested lists). The shape of array is a tuple of integers giving the size of the array along each dimension( e.g tuple(a,b) where a is row and b is column). we will see examples further stay tuned

you can easily turn a regular Python list, like [1, 2, 3, 4, 5, 6], into a NumPy array like this:

import numpy as np

a = np.array([1, 2, 3, 4, 5, 6])

Creating NumPy Arrays:

In this guide, we will explore the process of creating NumPy arrays.

• np.array()

The np.array() function is used to create a NumPy array from an existing sequence, like a Python list.

Example:

import numpy as np
my_list = [1, 2, 3, 4, 5]
my_array = np.array(my_list)

• np.zeros()

• The np.zeros() generates an array filled with zeros of a specified shape and data type.

• Usage: np.zeros(shape, dtype=float)

• Example:

    import numpy as np
    zeros_array = np.zeros((3, 4))  # Creates a 3x4 array filled with zeros
  

  

• np.ones()

Similar to np.zeros(), np.ones() creates an array with all elements initialized to 1.

• Example:

    import numpy as np
    ones_array = np.ones((3, 4))  # Creates a 2x3 array filled with ones
  

  

• np.arange()

The np.arange() creates an array with evenly spaced values within a specified range.

• Usage: np.arange(start, stop, step)

• Example:

    import numpy as np
    sequence = np.arange(0, 10, 2) 
     # Creates an array [0, 2, 4, 6, 8]
  

• np.linspace()

np.linspace() generates an array with num evenly spaced values between start and stop, including both start and stop values.

• Usage: np.linspace(start, stop, num)

Example:

import numpy as np
linspace_array = np.linspace(0, 1, 5)  
# Creates an array [0.  0.25 0.5 0.75 1.]

NumPy's Attributes:

One key aspect of NumPy's versatility is its extensive set of attributes that provide valuable information about arrays. These attributes offer insights into the array's characteristics, shape, and content, making them invaluable for data analysis and manipulation.

• np.shape

It reveals how many rows and columns an array has, providing a crucial clue for understanding its structure.

import numpy as np
my_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(my_array.shape)  # Output: (3, 4)

• np.ndim

How many dimensions does your array have? ndim has the answer. It tells you if it's a 1D array, 2D matrix, or something even grander.

import numpy as np
my_array = np.array([1, 2, 3, 4])
print(my_array.ndim)  # Output: 1

• np.size

size provides the total number of elements in your array.

import numpy as np
my_array = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print(my_array.size)  # Output: 12

• np.dtype

What kind of data is stored in your array? The dtype attribute reveals the data type, whether it's integers, floats, booleans, or more.

import numpy as np
my_array = np.array([1, 2, 3, 4], dtype=float)
print(my_array.dtype)  # Output: float64

Operation on array:

In this section, we will explore some of the core statistical operations that NumPy offers. These operations, including finding the maximum, minimum, sum, mean, product, and standard deviation of your data, serve as the building blocks of data analysis and provide valuable insights into your datasets.

• Maximum and Minimum: np.max() and np.min()

NumPy's np.max() and np.min() functions allow you to find the maximum and minimum values in an array with ease.

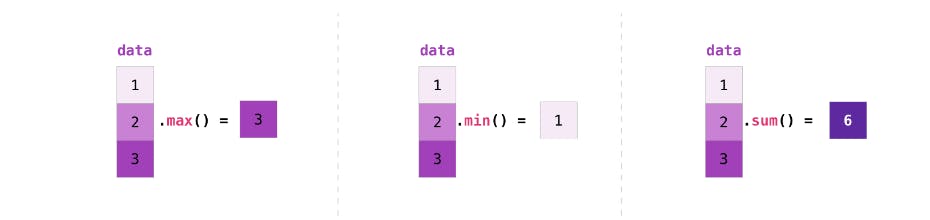
• Summation: np.sum()

Summation is a fundamental operation in data analysis. You can calculate the sum of array elements using np.sum().

• Mean: np.mean()

The mean (average) provides insight into the central tendency of your data.

• Product: np.prod()

You can compute the product of array elements using np.prod().

• Standard Deviation: np.std()

Standard deviation measures the spread or dispersion of data.

• Statistical functions: np.var(), np.median(), np.percentile()

NumPy offers more advanced statistical functions like np.var() for variance, np.median() for median, and np.percentile() for calculating percentiles, which are valuable for in-depth data analysis.

Here's a single code snippet that demonstrates the use of NumPy for maximum, minimum, sum, mean, product, and standard deviation calculations:

import numpy as np

data = np.array([5, 2, 8, 1, 6])

# Find the maximum and minimum
maximum = np.max(data)  # Maximum: 8
minimum = np.min(data)  # Minimum: 1

# Find the sum
total = np.sum(data)  # Sum: 22

# Find the mean (average)
average = np.mean(data)  # Mean: 4.4

# Find the product
product = np.prod(data)  # Product: 480

# Find the standard deviation
std_deviation = np.std(data)  # Standard Deviation: 2.701851217221259

# Print the results
print("Maximum:", maximum)
print("Minimum:", minimum)
print("Sum:", total)
print("Mean:", average)
print("Product:", product)
print("Standard Deviation:", std_deviation)

Data manipulation:

• np.sort()

  NumPy's np.sort() function allows you to sort the elements of an array along a specified axis. Here's how it works:

import numpy as np

my_array = np.array([3, 1, 2, 4, 5])
sorted_array = np.sort(my_array)
print(sorted_array)  # Output: [1 2 3 4 5]

By default, np.sort() performs an ascending sort. You can also sort in descending order:

import numpy as np

my_array = np.array([3, 1, 2, 4, 5])
descending_sorted_array = np.sort(my_array)[::-1]
print(descending_sorted_array)  # Output: [5 4 3 2 1]

• np.concatenate()

Sometimes, you need to merge two or more arrays to create a larger one. NumPy's np.concatenate() function allows you to do just that. You can concatenate arrays along specified axes.

import numpy as np

array1 = np.array([1, 2, 3])
array2 = np.array([4, 5, 6])
combined_array = np.concatenate((array1, array2))
print(combined_array)  # Output: [1 2 3 4 5 6]

For multi-dimensional arrays, you can concatenate along different axes:

import numpy as np

array1 = np.array([[1, 2], [3, 4]])
array2 = np.array([[5, 6]])
combined_array = np.concatenate((array1, array2), axis=0)#0 means row wise
print(combined_array)
# Output:
# [[1 2]
#  [3 4]
#  [5 6]]

• np.put()

The . put() function replaces specific elements of an array with given values of p_array. Array indexed works on the flattened array.

import numpy as np

array1 = np.array([3,2,3,4,5,6,7])
np.put(array1,[0,1],[11,12])
print(array1) #Output:[11 12  3  4  5  6  7]

Indexing and Slicing:

In this section, we'll dive into indexing and slicing of a numpy array. You can index and slice NumPy arrays in the same ways you can slice Python lists.

Indexing in NumPy

Indexing is all about pinpointing and extracting individual elements from an array. In NumPy, you can access elements using square brackets [ ] and specifying the index position. Here's how it works:

import numpy as np

my_array = np.array([1, 2, 3, 4, 5])
element = my_array[2]  # Access the element at index 2
print(element)  # Output: 3

NumPy also supports negative indexing, which counts elements from the end of the array:

import numpy as np

my_array = np.array([1, 2, 3, 4, 5])
element = my_array[-1]  # Access the last element
print(element)  # Output: 5

Slicing numpy array

Slicing allows you to cut out portions of an array. In NumPy, you use a colon : within the square brackets to define a slice. The syntax is start:stop:step, where start is the beginning index, stop is the end index (exclusive), and step is the spacing between elements. Here are some examples:

import numpy as np

my_array = np.array([1, 2, 3, 4, 5])
subset = my_array[1:4]  # Get elements from index 1 to 3
print(subset)  # Output: [2 3 4]

You can omit start, stop, or step to use default values:

import numpy as np

my_array = np.array([1, 2, 3, 4, 5])
subset = my_array[:3]  # Get elements from the beginning to index 2
print(subset)  # Output: [1 2 3].

Broadcasting:

There are times when you might want to carry out an operation between an array and a single number (also called an operation between a vector and a scalar) or between arrays of two different sizes.

Broadcasting is NumPy's way of making arrays with different shapes compatible for element-wise operations. It does this by automatically adjusting the shape of smaller arrays to match the shape of larger ones.

Here's a simple example to illustrate broadcasting:

import numpy as np

arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])

result = arr1 + arr2
print(result)  # Output: [5 7 9]

Concept of Broadcasting:

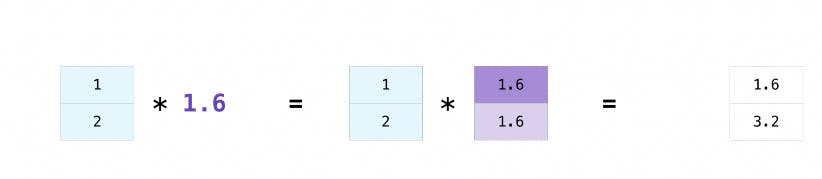
NumPy follows specific rules when performing broadcasting:

Conclusion:

In this journey through NumPy's powerful capabilities for data manipulation and analysis, we've explored indexing, slicing, broadcasting, and a range of essential statistical operations.

References: To continue your exploration and deepen your understanding of NumPy, here is the reference and resources of the blog:

1. NumPy Official Documentation: The official NumPy documentation provides comprehensive information, tutorials, and examples. NumPy Documentation

   

2. NumPy Cheatsheet: A handy cheatsheet with commonly used NumPy functions. NumPy Cheatsheet

"In a nutshell, NumPy is your go-to tool for unleashing the full potential of data manipulation and analysis in Python."